Strategies for Classification Layer Initialization in Model-Agnostic Meta-Learning
This blog post discusses different strategies for initializing the classification layers parameters before fine-tuning on a new task in Model-Agnostic Meta-Learning.
Introduction
In a previous study, Raghu et al. [2020]
First, it is difficult to imagine that a single set of optimal weights can be learned. This becomes apparent when considering class label permutations: two different tasks may have the same classes but in a different order. As a result, the weights that perform well for the first task will likely not be effective for the second task. This is reflected in the fact that MAML’s performance can vary by up to 15% depending on the class label assignments during testing
Second, more challenging datasets are being proposed as few-shot learning benchmarks, such as Meta-Dataset
Therefore, it seems logical to consider how to initialize the final classification layer before fine-tuning on a new task. Random initialization may not be optimal, as it can introduce unnecessary noise
This blog post will discuss different approaches to last layer initialization that claim to outperform the original MAML method.
Quick recap on MAML
Model-Agnostic Meta-Learning (MAML)
where $\alpha$ is the inner loop learning rate, $\mathcal{L_{\mathcal{T_{i}}}}$ is a task’s loss function, and $\mathcal{D^{tr}}$ is a task’s training set. The task includes a test set as well: $\mathcal{T_{i}} = (\mathcal{D_{i}^{tr}}, \mathcal{D_{i}^{test}})$.
In the outer loop, the meta parameter $\theta$ is updated by backpropagating through the inner loop to reduce errors made on the tasks’ test set using the fine-tuned parameters:
\[\theta' = \theta - \eta\nabla_{\theta} \sum_{\mathcal{T_{i}} \sim p(\mathcal{T})}^{} \mathcal{L_{\mathcal{T_{i}}}}(\theta_{i}', \mathcal{D^{test}}).\]Here, $\eta$ is the meta-learning rate. The differentiation through the inner loop involves calculating second-order derivatives, which mainly distinguishes MAML from simply optimizing for a $\theta$ that minimizes the average task loss.
It is worth noting that in practical scenarios, this second-order differentiation is computationally expensive, and approximation methods such as first-order MAML (FOMAML)
Before proceeding, let’s prepare ourselves for the next sections by looking at the notation we can use when discussing MAML in the few-shot classification regime: The model’s output prediction can be described as $\hat{y} = f_{\theta}(\mathbf{x}) = \underset{c\in[N]}{\mathrm{argmax}} ; h_{\mathbf{w}} (g_{\phi}(\mathbf{x}), c)$, where we divide our model $f_{\theta}(\mathbf{x})$ (which takes an input $\mathbf{x}$) into a feature extractor $g_{\phi}(\mathbf{x})$ and a classifier $h_\mathbf{w}(\mathbf{r}, c)$, which is parameterized by classification head weight vectors ${\mathbf{w}}_{c=1}^N$. $\mathbf{r}$ denotes an input’s representation, and $c$ is the index of the class we want the output prediction for.
Finally, $\theta = {\mathbf{w_1}, \mathbf{w_1}, …, \mathbf{w_N}, \phi}$, and we are consistent with our previous notation.
Learning a single initialization vector
The first two variants of MAML - we look at - approach the initialization task by initializing the classification head weight vectors uniformly for all classes. In the paper
▶ Han-Jia Ye & Wei-Lun Chao (ICLR, 2022) How to train your MAML to excel in few-shot classification
an approach called UnicornMAML is presented. It is explicitly motivated by the effect that different class-label assignments can have. Ye & Chao [2022]
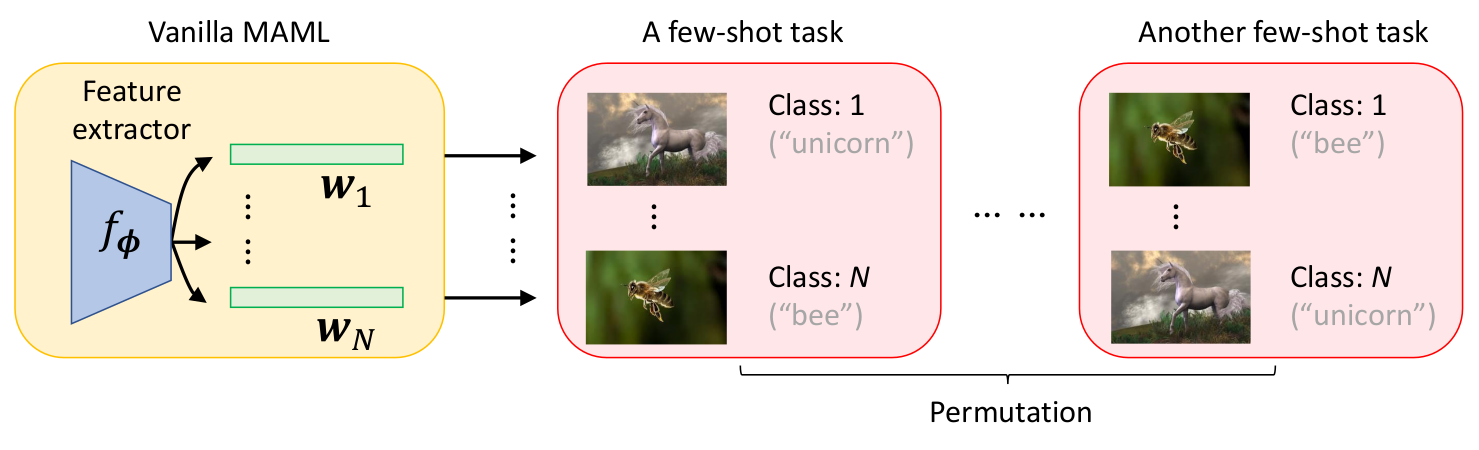
Fig.1 Example of MAML and a class label permutation. We can see the randomness introduced, as $\mathbf{w_1}$ is supposed to interpret the input features as "unicorn" for the first task, and as "bee" for the second. For both tasks, the class outputted as a prediction should be the same, as in human perception, both tasks are identical. This, however, is obviously not the case.
The solution proposed is fairly simple: Instead of meta-learning $N$ weight vectors for the final layer, only a single vector $\mathbf{w}$ is meta-learned and used to initialize all $ \{ \mathbf{w} \}_{c=1}^N $ before the fine-tuning stage.
This forces the model to make random predictions before the inner loop, as $\hat{y_c}= h_{\mathbf{w}} (g_{\phi} (\mathbf{x}), c)$ will be the same for all $c \in [1,…,N ]$.
After the inner loop, the updated parameters have been computed as usual: \(\theta' = \\{\mathbf{w_1}', \mathbf{w_2}', ..., \mathbf{w_N}', \phi'\\}\). The gradient for updating the single classification head meta weight vector $\mathbf{w}$, is just the aggregation of the gradients w.r.t. all the single $\mathbf{w_c}$:
\[\nabla_{\mathbf{w}} \mathcal{L_{\mathcal{T_i}}} (\mathcal{D^{test}}, \theta_i) = \sum_{c \in [N]} \nabla_{\mathbf{w_c}} \mathcal{L_{\mathcal{T_i}}} (\theta_i, \mathcal{D^{test}})\]This collapses the models meta-parameters to $ \theta = \{\mathbf{w}, \phi\} $.
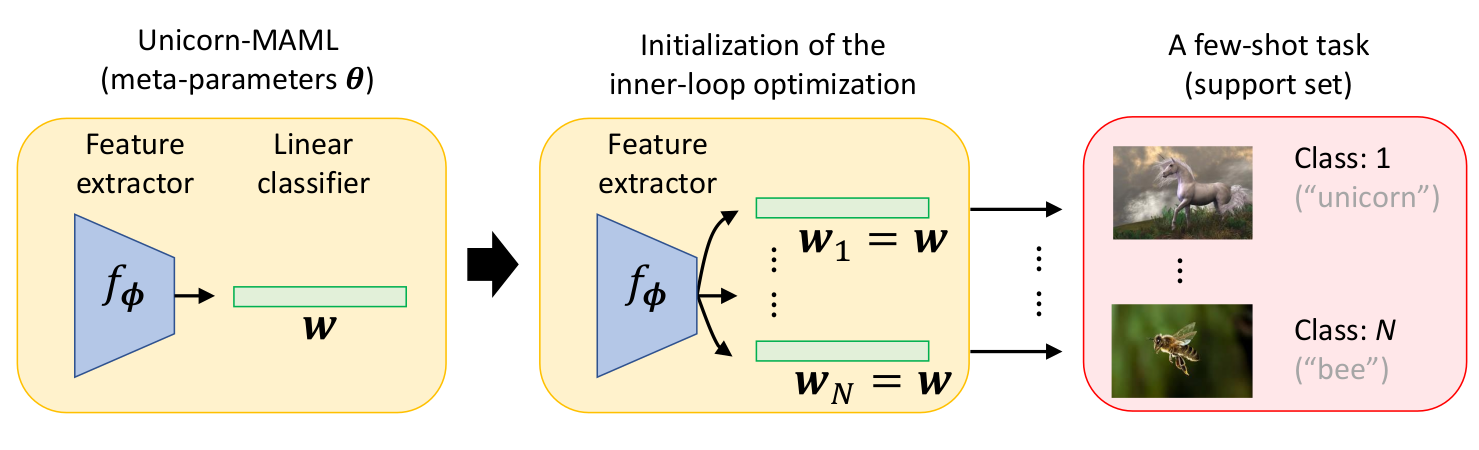
Fig.2 Overview of UnicornMAML. We can see that class label permutations don't matter anymore, as before fine-tuning, the probability of predicting each class is the same.
This tweak to vanilla MAML makes UnicornMAML permutation invariant, as models fine-tuned on tasks including the same categories - just differently ordered - will now yield the same output predictions. Also, the method could be used with datasets where the number of classes varies without any further adaptation: It doesn’t matter how many classification head weight vectors are initialized by the single meta-classification head weight vector.
Furthermore, the uniform initialization in Unicorn-MAML addresses the problem of memorization overfitting
The approach is reported to perform on par with recent few-shot algorithms.
Let’s finally think of how to interpret UnicornMAML: When meta-learning only a single classification head vector, one could say that not a mapping from features to classes is tried to be learned any more, but a prioritization of features, which seemed to be more relevant for the classification decision across tasks, than others.
Zero initialization
The second approach for a uniform initialization is proposed in the paper
▶ Chia-Hsiang Kao et al. (ICLR, 2022) MAML is a Noisy Contrastive Learner in Classification
Kao et al. [2022]
An overview of MAML with the zeroing trick is displayed below:

Fig.3 MAML with the zeroing trick applied.
Note that $S_n$ and $Q_n$ refer to $\mathcal{D_{i}^{tr}}$ and $\mathcal{D_{i}^{test}}$ in this notation.
Through applying the zero initialization, three of the problems addressed by UnicornMAML are solved as well:
- MAML with the zeroing trick applied leads to random predictions before fine-tuning. This solves the problem of class label assignment permutations during testing.
- Through the random predictions before fine-tuning, memorization overfitting is prevented as well.
- The zeroing trick makes MAML applicable for datasets with a varying number of classes per task.
Interestingly, the motivation for applying the zeroing trick, stated by Kao et al. [2022]
More specifically, they show that the outer-loop update for the encoder follows a noisy SCL loss under the following assumptions:
- The encoder weights are frozen in the inner loop (EFIL assumption)
- There is only a single inner loop update step.
Note that FOMAML technically follows a noisy SCL loss without this assumption. However, when applying the zeroing trick, this assumption is needed again for stating that the encoder update is following an SCL loss
A noisy SCL loss means that cases can occur where the loss forces the model to maximize similarities between embeddings from samples of different classes. The outer-loop encoder loss in this setting contains an “interference term” which causes the model to pull together embeddings from different tasks or to pull embeddings into a random direction, with the randomness being introduced by random initialization of the classification head. Those two phenomena are termed cross-task interference and initialization interference. Noise and interference in the loss vanish when applying the zeroing trick, and the outer-loop encoder loss turns into a proper SCL loss. Meaning that minimizing this loss forces embeddings of the same class/task together while pushing embeddings from the same task and different classes apart. A decent increase in performance is observed for MAML with the zeroing trick compared to vanilla MAML.
Those findings are derived using a general formulation of MAML, with a cross-entropy loss, and the details are available in the paper
MAMLs SCL Intuition
To get an intuition of how MAML relates to SCL, let’s look at the following setup: an N-way one-shot classification task using MAML with Mean Squared Error (MSE) between the one-hot encoded class label and the prediction of the model. Furthermore, the EFIL assumption is made, the zeroing trick is applied, only a single inner loop update step is used, and only a single task is sampled per batch.
In this setting, the classification heads inner-loop update for a single datapoint looks like this:
\[\mathbf{w}' = \mathbf{w} - \alpha (-g_{\phi} (\mathbf{x}_{1}^{tr}) \mathbf{t}_{1}^{tr\top})\]$\mathbf{t}_1^{tr}$ refers to the one-hot encoded class label belonging to $\mathbf{x}_1^{tr}$. In words, the features extracted for training example $\mathbf{x}_1^{tr}$ are added to column $\mathbf{w}_c$, with $c$ being the index of 1 in $\mathbf{t}_1^{tr}$. For multiple examples, the features of all training examples labeled with class $c$ are added to the $c^{th}$ column of $\mathbf{w}$.
Now, for calculating the model’s output in the outer loop, the model computes the dot products of the columns \(\\{\mathbf{w} \\}_{c=1}^N\) and the encoded test examples \(g_{\phi}(\mathbf{x}_1^{test})\) (and takes a softmax afterward.) To match the one-hot encoded label as good as possible, the dot product has to be large when \(\mathbf{t}_1^{test}\) = \(1\) at index \(c\), and small otherwise. We can see that the loss enforces embedding similarity for features from the same classes while enforcing dissimilarity for embeddings from different classes, which fits the SCL objective.
Initialization using prototypes
A more sophisticated approach for last-layer initialization in MAML is introduced in the paper
▶ Eleni Triantafillou et al. (ICLR, 2020) Meta-Dataset: A Dataset of Datasets for Learning to Learn from Few Examples
As one might guess from the name, Proto-MAML makes use of Prototypical Networks (PNs) for enhancing MAML. Opposite to the two initialization strategies presented above, Proto-MAML does not uniformly initialize the classification head weights before each inner loop for all classes. Instead, it calculates class-specific initialization vectors based on the training examples. This solves some of the problems mentioned earlier (see Conclusion & Discussion), but also it adds another type of logic to the classification layer.
Let’s revise how PNs work when used for few-shot learning for understanding Proto-MAML afterward:
Class prototypes \(\mathbf{c}_{c}\) are computed by averaging over train example embeddings of each class, created by a feature extractor \(g_{\phi}(\mathbf{x})\). For classifying a test example, a softmax over the distances (e.g., squared euclidean distance) between class prototypes \(\mathbf{c}_{c}\) and example embeddings \(g_{\phi}(\mathbf{x}^{test})\) is used, to generate probabilities for each class.
When using the squared euclidean distance, the model’s output logits are expressed as:
\[\begin{align*} &- \vert \vert g_{\phi}(\mathbf{x}) - \mathbf{c}_c \vert \vert^2 \\ =& −g_{\phi}(\mathbf{\mathbf{x}})^{\top} g_{\phi}(\mathbf{x}) + 2 \mathbf{c}_{c}^{\top} g_{\phi}(\mathbf{x}) − \mathbf{c}_{c}^{\top} \mathbf{c}_{c} \\ =& 2 \mathbf{c}_{c}^{\top} g_{\phi}(\mathbf{x}) − \vert \vert \mathbf{c}_{c} \vert \vert^2 + constant. \end{align*}\]Note that the “test” superscripts on $\mathbf{x}$ are left out for clarity. \(−g_{\phi}(\mathbf{x})^{\top} g_{\phi}(\mathbf{x})\) is disregarded here, as it’s the same for all logits, and thus doesn’t affect the output probabilities. When inspecting the left-over equation, we can see that it now has the shape of a linear classifier. More specifically, a linear classifier with weight vectors \(\mathbf{w}_c = 2 \mathbf{c}_c^{\top}\) and biases \(b_c = \vert \vert \mathbf{c}_{c} \vert \vert^2\).
Proceeding to Proto-MAML, Triantafillou et al. [2020]
Note that because of computational reasons, Triantafillou et al. [2020]
With Proto-MAML, one gets a task-specific, data-dependent initialization in a simple fashion, which seems super nice. For computing the model’s output logits after classification head initialization, dot products between class prototypes and embedded examples are computed, which again seems very reasonable.
One could argue that in the one-shot scenario, Proto-MAML doesn’t learn that much in the inner loop beside the initialization itself. This happens as the dot product between an embedded training example and one class prototype (which equals the embedded training example itself for one class) will be disproportionately high. For a k-shot example, this effect might be less, but still, there is always one training example embedding within the prototype to compare. Following this thought, the training samples would rather provide a useful initialization of the final layer than a lot of parameter adaptation. One has to say that Proto-MAML performed quite well in the authors’ experiments.
What else is there?
Before proceeding to Conclusion & Discussion, here are some pointers to methods that did not perfectly fit the topic but which are closely related:
The first method worth mentioning is called Latent Embedding Optimization (LEO)
LEO deviates from the initialization scheme, however, as optimization is done in the low dimensional subspace and not on the model’s parameters directly. It is stated that optimizing in a lower dimensional subspace helps in low-data regimes.
Another related method is called MetaOptNet
Conclusion & Discussion
To conclude, we’ve seen that a variety of problems can be tackled by using initialization strategies for MAMLs linear classification head, including:
- Varying performance due to random class label assignments
- Ability of MAML to work on datasets where the number of classes per task varies
- Memorization overfitting
- Cross-task interference
- and Initialization interference.
Furthermore, for all the approaches presented, a decent gain in performance is reported in comparison to vanilla MAML. It seems, therefore, very reasonable to spend some time thinking about the last layer initialization.
Looking at the problems mentioned and variants discussed in more detail, we can state that all the different variants make MAML permutation invariant with regard to class label assignments. UnicornMAML and the zeroing trick solve it by uniform initialization of $\mathbf{w}$. In Proto-MAML, the initialization happens with regard to the class label assignment, so it’s permutation invariant as well.
Also, all variants are compatible with datasets where the number of classes per task varies. In UnicornMAML, an arbitrary number of classification head vectors can be initialized with the single meta-learned classification head weight vector. When zero-initializing the classification head, the number of classes per task does not matter as well. In Proto-MAML, prototypes can be computed for an arbitrary number of classes, so again, the algorithm works on such a dataset without further adaption.
Next, UnicornMAML and the zeroing trick solve memorization overfitting, again by initializing $\mathbf{w}$ uniformly for all classes. Proto-MAML solves memorization overfitting as well, as the task-specific initialization of $\mathbf{w}$ itself can be interpreted as fine-tuning.
Cross-task interference and initialization interference are solved by the zeroing trick. For the other models, this is harder to say, as the derivations made by Kao et al. are quite a case specific. Intuitively, Proto-MAML should solve cross-task interference, as the classification head is reinitialized after each task. Initialization interference is not solved by either ProtoMAML or UnicornMAML, as random initialization remains.
Note that in discussion with a reviewer, Kao et al. state that the main results they show are achieved by models which had the zeroing trick implemented but which didn’t follow the EFIL assumption. They argue that using only the zeroing trick still enhances supervised contrastiveness. This kind of puts their whole theory into perspective, as without the EFIL assumption, MAML with the zeroing trick is neither an SCL algorithm nor a noisy SCL algorithm. Still, noticeable performance gains are reported though.
The question arises whether the whole theoretical background is needed or whether the zeroing tricks benefit is mainly the uniform initialization, like in UnicornMAML. It would be nice to see how the single learned initialization vector in UnicornMAML turns out to be shaped and how it compares to the zeroing trick. While the zeroing trick reduces cross-task noise and initialization noise, a single initialization vector can weight some features as more important than others for the final classification decision across tasks.
In contrast to the uniform initialization approaches, we have seen Proto-MAML, where class-specific classification head vectors are computed for initialization based on the training data.
Finally, Ye et al. [2022]